債券存續期間是什麼？債券存續期間與利率變動的關係？

最後更新：2023-03-16

在談到債券時，常聽到的一個名詞就是存續期間(Duration)，但很多人對其一知半解，至把它債券「到期時間Average effective maturity」搞混。

投資債券時，利率變化是一個造成風險的主因，存續期間，是債券、債券基金、債券ETF，用來衡量到底利率上升下降對債券影響的重要指標。

這篇文章市場先生介紹存續期間(Duration)，包含以下幾個部分：

債券存續期間是什麼？

債券存續期使用上的定義：存續期間是衡量利率變動的參數

債券的存續期間一般用來衡量債券價格對市場利率的敏感度，實際應用上存續期間的意義就是說市場利率每變動1%，那麼債券價格預期會變動多少%。

債券的「存續期間 Duration」跟「到期時間 Maturity」常會被混淆，債券的到期時間(債券基金/ETF因為是一籃子債券，是看平均到期時間)雖然單位也是年，和存續期間也成正比，但並沒有評估利率影響的功能。

債券存續期在計算上的定義：存續期間是持有債券的平均回本時間

債券的存續期間(Duration)計算公式上的定義是「持有債券的平均回本時間」。

亦即投資人買了債券後，以總現金流來回收債券本息所需要的時間，以「年」為單位，採加權平均計算。

如果是有付息的債券，因為過程中有現金流，那麼存續期間會比到期時間短，

如果是零息債券，因為過程中沒有現金流，存續期間就會等於到期時間。

以下用一個簡單方式說明(但非實際算法，教學使用先簡化)：

假如花10,000元買一張債券，二年到期，一年後拿回5,000元，二年後再拿回另外5,000元，
那麼拿回本所需要的平均年限為(1*5,000+2*5000)/10,000=1.5年，這1.5年就是債券的存續期間。

但計算上的定義比較不重要，一般我們不需要自己算，各種債券投資標的都有公開資料自動幫我們算好，我們只需要知道它的用途和怎麼查就夠了。

會影響債券存續期間的因素

1. 到期日：到期日越長，存續期間越長
2. 票面利率：票面利率越高，存續期間越短(因為領的利息越多，回本時間越短)
3. 到期殖利率(Yield to Maturity)：到期殖利率越高，存續期間越短(收益率高回本速度快）

債券存續期間與利率的關係

上面提到債券的存續期間是用來衡量債券價格對利率的敏感度，存續期間越長，對利率變動的敏感度越大，

那麼在預期市場利率變動時，配置什麼樣的債券才是對投資人最有利的呢？

債券價格跟利率的關係就像是翹翹板，

• 市場利率上升，債券價格下跌：
  如果預期市場利率上升，投資人應該縮短手上債券的存續期間，因為存續期間越短，跌幅越小。
• 市場利率下跌，債券價格上升：
  如果預期市場利率下跌，此時投資人應該增加手上債券的存續期間，因為存續期間越長，升幅越大。

至於升幅、跌幅到底有多大，存續期間就是反應這點的指標。

假設存續期間是7(年)，代表利率上升1%，這個債券組合會下跌7%，利率下降1%，則債券組合上漲7%。

這個上漲下跌幅度是個大略估計值，而不會是實際狀況。而真實市場中由於價格仍會反應人們對未來複雜的預期，因此漲跌程度必然有一定的誤差空間，結果不會如同計算公式一樣精確。

市場先生整理存續期間應用的小結：

1. 存續期間越長的債券，受利率影響的敏感度就越大，利率變動時易有大波動。反之存續期間短的債券，受利率影響也比較小。簡單來說，長期債券利率風險高(大漲大跌)、短期債券利率風險低(小漲小跌)。

2. 未來利率若上升超乎預期時，存續期間高的債券下跌比較多、存續期間低的債券下跌比較少。反之，未來利率若下降超乎預期時，存續期間高的債券上漲比較多、存續期間低的債券上漲比較少。

以下是計算部分，由於存續期間其實都查的到，因此市場先生的看法是你不需要會計算，只要知道概念就可以了。

債券的存續期間是如何計算？

在實務上存續期間有兩種常用的計算方式，

• 麥考利存續期間(Macaulay Duration)
• 修正存續期間(Modified Duration)

麥考利存續期間是由Frederick Macaulay在1938年所提出，後人依此命名。

存續期間的計算方式有點小複雜，以下盡量用最簡單的方式說明，如果對數學計算沒有興趣的，也
可以跳過這段直接使用文末附上的連結，輸入相關數據後即可自動計算。

麥考利存續期間(Macaulay Duration)計算方式

麥考利存續期間是支付債券所有的現金流的加權平均時間，以年計算，

它考慮了未來債券現金流的現值(present value)，可以幫助投資者評估及比較不同到期日債券。

其計算方式舉例如下：

假設某債券票面金額是10,000，票面利率2%，五年後到期，到期殖利率是3%

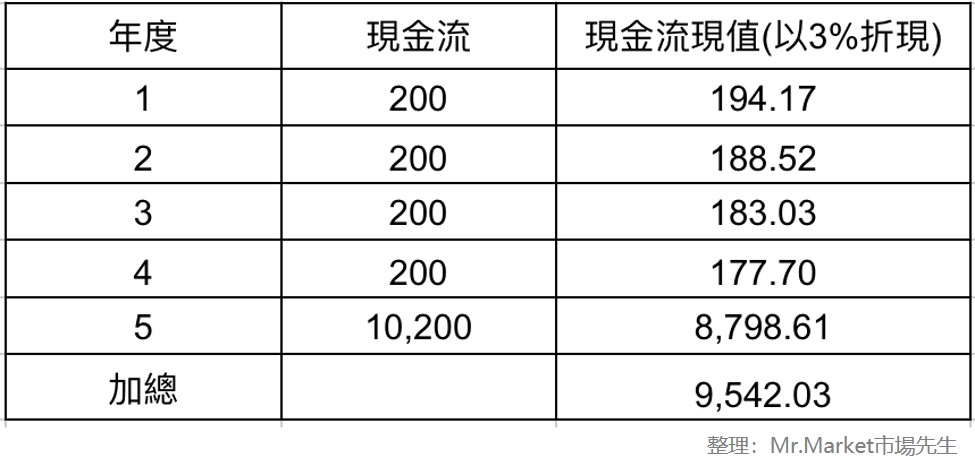
步驟1：計算債券利息和本金的現金流現值

計算出來的現金流現值加總9,542.03即為債券現值

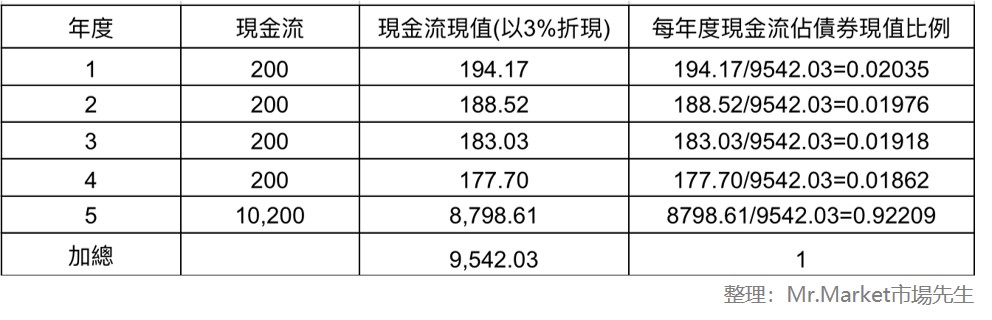
步驟2：計算每年度現金流現值佔債券現值的比例

用每年度現金流現值除債券現值9,542.03即可得到佔比

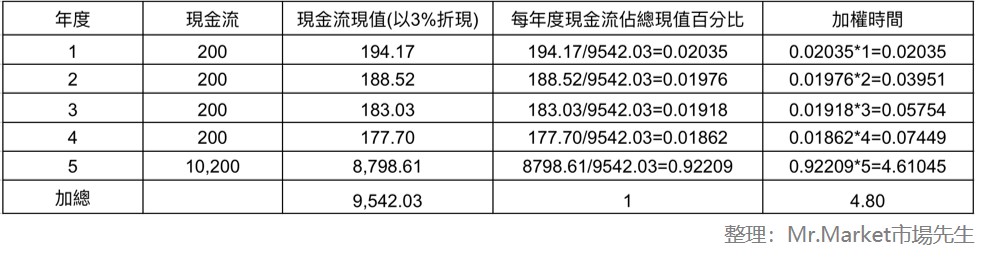
步驟3：計算出加權時間

用每年度現金流佔債券現值佔比乘上年度，即可得到加權時間，

各年度加權時間加總得到債券存續期間是4.8年，意思是市場利率每變動1%，債券價格預期會變動4.8%。

債券存續期間可到鉅亨網上面快速試算，

只要輸入債券購買日期、債券到期日、債券面額、購買價格、票面利率、
每年付息次數、殖利率，就可以得到債券存續期間。
殖利率如果不知如何計算，在同一個頁面最上方直接輸入債券資料就可以試算。

修正存續期間(Modified Duration)計算方式

修正存續期間和麥考利存續期間不同，單位不是年，但它也是用來衡量如果利率變化1%，債券價格預期會改變多少，

計算公式是用麥考利存續期間算出來的數字/(1+到期殖利率/年配息次數)。

例如上面那個案例，麥考利存續期間是4.8年，到期殖利率3%、年配息次數1次，
那麼它的修正存續期間就是：4.8/(1+0.03/1)=4.66

這代表如果市場利率上升1%，債券價格預估會下跌4.66%，
不過這是估計值而已，實際狀況如果利率變動越大，用修正存續期間來預估會越不準確。

快速重點整理：債券存續期間是什麼？

1. 債券存續期間是指持有債券的平均回本時間，以現金流的現值加權計算，可用來衡量債券價格對利率的敏感度，如果市場利率變動1%，債券價格會變動多少。存續期間越長的債券，對利率變化的敏感度會越高。
2. 在預期市場利率上升時，債券會下跌，存續期間長的債券會下跌相對更多；在預期市場利率下跌時，債券會上漲，存續期間長的債券預期也會上漲更多。
3. 債券存續期間計算方式有兩種：麥考利存續期間跟修正存續期間，一般人要自我計算較為複雜，建議可用既有網站直接試算即可。

專欄作者：牟均俞　主編：市場先生

債券其實是個很好用的投資工具，但也必須正確使用才行，
更多債券文章可閱讀：

1. 什麼是債券，有哪些投資方式？

2. 認識5檔美國公債ETF

3. 美國市政債是什麼？如何投資？

4. 為什麼高收益債沒有避險功能？

5. 美股常用券商開戶推薦比較

加入市場先生FB社團，充實更多理財好知識

50歲之前想退休一定要懂理財，
解決投資的煩惱！

最近市場先生開了一堂的「用美股ETF創造穩定現金流」教學課程，
這堂課程會從基礎入門、資料查詢到實際操作，
教你學會建立一個穩定的全球ETF投資組合，目前累積已經有將近1100位同學上課。

線上課程》美股ETF創造穩定現金流線上課程連結

如果覺得這篇文章有幫助，
幫我按個讚，分享給更多人看到，謝謝！