到期殖利率(YTM)、票面利率是什麼?一次介紹債券的4種利率
買債券前有一件很重要的事,就是要搞懂債券的4個利率(票面利率、當期殖利率、到期殖利率、贖回殖利率),其中最重要的是到期殖利率(YTM)。
這4種利率聽起來很相似,但意義差距卻可能很遠。本篇市場先生將一次介紹這4種債券利率。
如果還不熟悉債券,在開始閱讀本篇,可先閱讀:債券是什麼?
本文市場先生會告訴你:
到期殖利率(YTM)是什麼?
到期殖利率(債券殖利率) = 買入債券一直持有至到期為止的實質投資報酬率。
在債券中談到殖利率,一般指的都是到期殖利率 (英文: Yield to Maturity,簡稱YTM),意思是考慮債券買入價格、未來可領取的利息、持有到期後拿回本金,所推算出的年化報酬率。
到期殖利率要用買入價格、利息、票面金額計算(可用excel算),舉例來說,一張債券定價是100元,票面利率是5%,以102元的價格買入,持有5年,最後可拿回本金100元,那麼計算出來的殖利率為4.54%。如下圖:
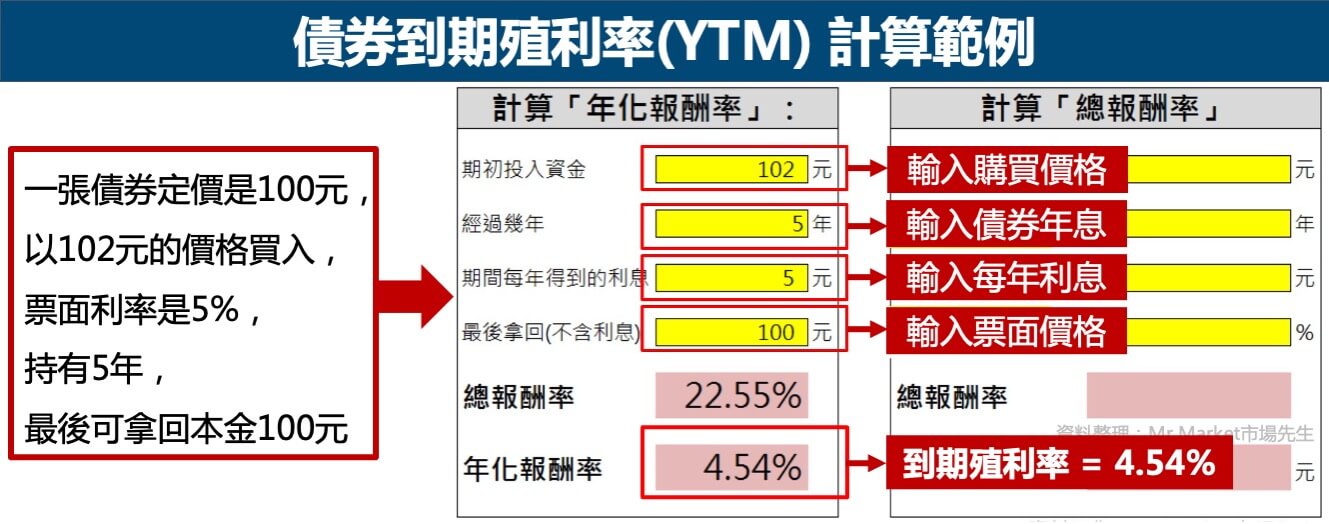
票面利率是什麼?
票面利率 = 每年利息 ÷ 債券面額
票面利率(英文: Coupon Rate)指的是債券在發行時,直接被印刷在債券票面上的應付利率。
假如一張債券的面額(Face Value)是100元,票面利率是5%,那麼每年投資人會收到的利息就是5元,到期時拿回本金100元。
要注意的是,債券面額不等於你買進債券的價格(買入價格),也就是說,面額是100元,但你買進的價格不一定是100元,價券交易價格是變動的,而面額和票面利率是不會變的。
在整個債券交易中,票面利率常常被用作話術,看似6%票面利率的債券,實際上如果你根據市價買入,到期殖利率(YTM)可能只有3%。
票面利率只是債券報酬計算過程用的數字,實際債券投資時,票面利率毫無任何意義。
市場先生補充:
當我們以溢價購入債券時,到期殖利率一定會小於票面利率,而當我們以低於票面價格購入債券時,到期殖利率會高於票面利率。
以美國公債為例,假設公債票面價值是100元:
- 當購入價格 = 100元,到期殖利率 = 票面利率
- 當購入價格 > 100元,到期殖利率 < 票面利率
- 當購入價格 < 100元,到期殖利率 > 票面利率
當期殖利率是什麼?
當期殖利率 = 每年利息 ÷ 買入價格
當期殖利率(英文: Current Yield)是考慮債券的買入價格,計算出當期的收益率。當買入價格大於票面價格時,當期殖利率會低於票面利率。
假如一張債券定價是100元,票面利率是5%,投資人以102元買入,那麼他每年會收到的利息為5元,當期殖利率=5÷102=4.9%。
當期殖利率只考量到了目前的收益,沒有考量到到期時拿回本金的損益,因此不是最好參考數字。(以上面這個案例來說,用102元買入,到期只有拿回100元本金,因此本金損失了2元,故實際的報酬率會低於4.9%)
贖回殖利率是什麼?
贖回殖利率 = 在債券未到期前就要出售,想要計算持有期間的報酬率時用的殖利率。
贖回殖利率 (英文: Yield to Call,簡稱YTC)意思是考量買入價格、已領取的利息、賣出價格來推算出的年化報酬率。
在持有過程中,雖然到期殖利率是固定的,但因債券交易價格是變動的,這代表你任何時間點提早賣出的話,報酬率也是隨時變動的。
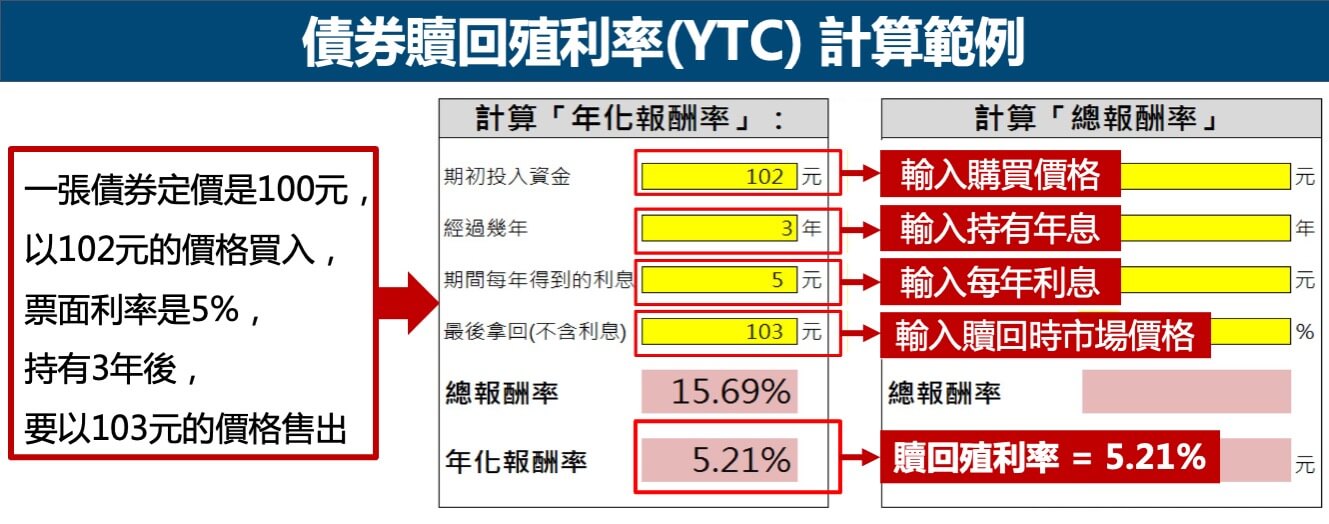
贖回殖利率要用買入價格、利息、贖回時市場價格計算(可用excel算),舉例來說,一張債券定價是100元,票面利率是5%,以102元的價格買入,持有3年後,要以103元的價格售出,那麼計算出來的贖回殖利率為5.21%。如下圖:
比較債券的4種利率
以下把票面利率、當期殖利率、到期殖利率、贖回殖利率做一個比較:
| 債券的4種利率比較 |
||
| 利率種類 | 計算方式 | 意思 |
| 票面利率 | 每年利息 ÷ 債券面額 | 債券在發行時,直接印在債券票面上的利率 |
| 當期殖利率 | 每年利息 ÷ 買入價格 | 考慮債券的買入價格,算出當期的收益率 (不會考量到期時拿回本金的損益) |
| 到期殖利率 YTM(重要) |
用買入價格、利息、票面金額計算 | 買入債券~到期為止的實質投資報酬率 |
| 贖回殖利率 YTC(重要) |
用買入價格、利息、贖回時市場價格計算 | 債券未到期前要出售,想計算持有期間的報酬率時使用 |
| 資料整理:Mr.Market市場先生 | ||
對於投資債券來說,購買時最重要的是看到期殖利率(YTM),在持有期間要出售則是要看贖回殖利率(YTC),票面利率跟當期殖利率並不重要。
特別提醒一下,在債券持有的過程中,如果債券價格上漲了,當下出售雖會比持有至到期賺更多,但決定我們是否要出售,不僅僅是考慮賣出有賺更多,而且還要考慮售出得到的現金,有沒有其他更好的投資機會?
因為售出後要再買相同的債券,市場價格也變貴了,換句話說,當下你雖然賺到錢,但那些現金不見得能再找到當初高殖利率的機會。
如果缺乏更好的投資機會,現金不能創造同等或更好報酬時,其實也可以考慮繼續持有債券。
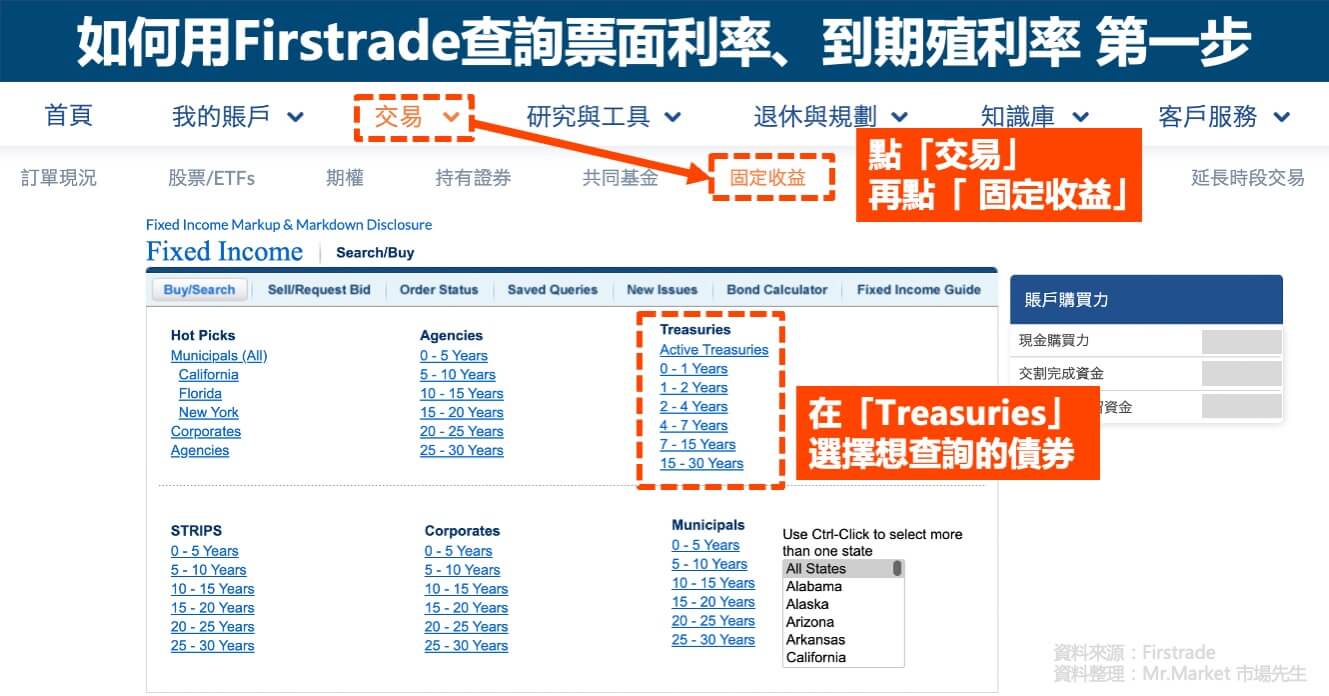
如何查詢債券的票面利率、到期殖利率?
一般來說,債券下單的介面都會揭露它的票面利率及到期殖利率,以下以Firstrade券商、IB盈透證券購買美國公債為例:
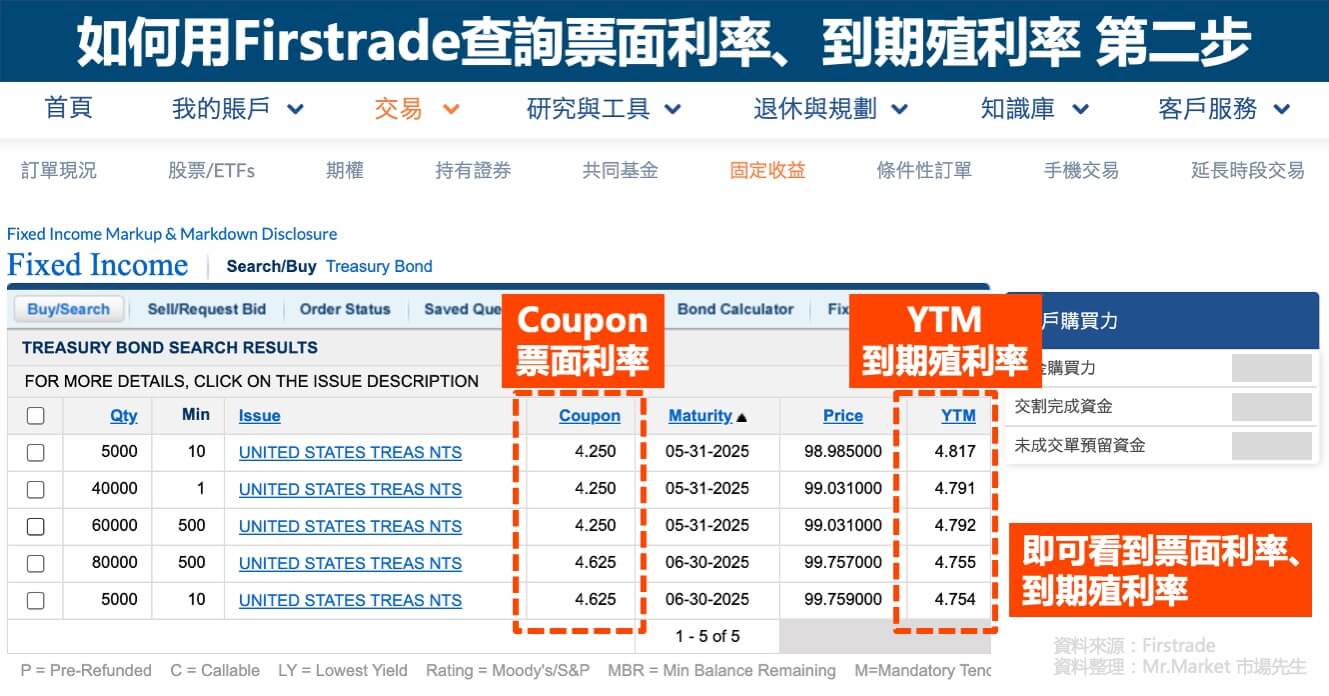
以Firstrade來說,債券的票面利率可以在「Coupon」這個欄位找到(但不重要),而到期殖利率則可在「YTM」這個欄位找到(看YTM是重點),總共兩個步驟,如下圖:
市場先生補充:
由上圖可以看到,差不多的存續期間,票面利率儘管有點不一樣,但會在價格(Price)上調整,所以最後到期殖利率還是差不多的。
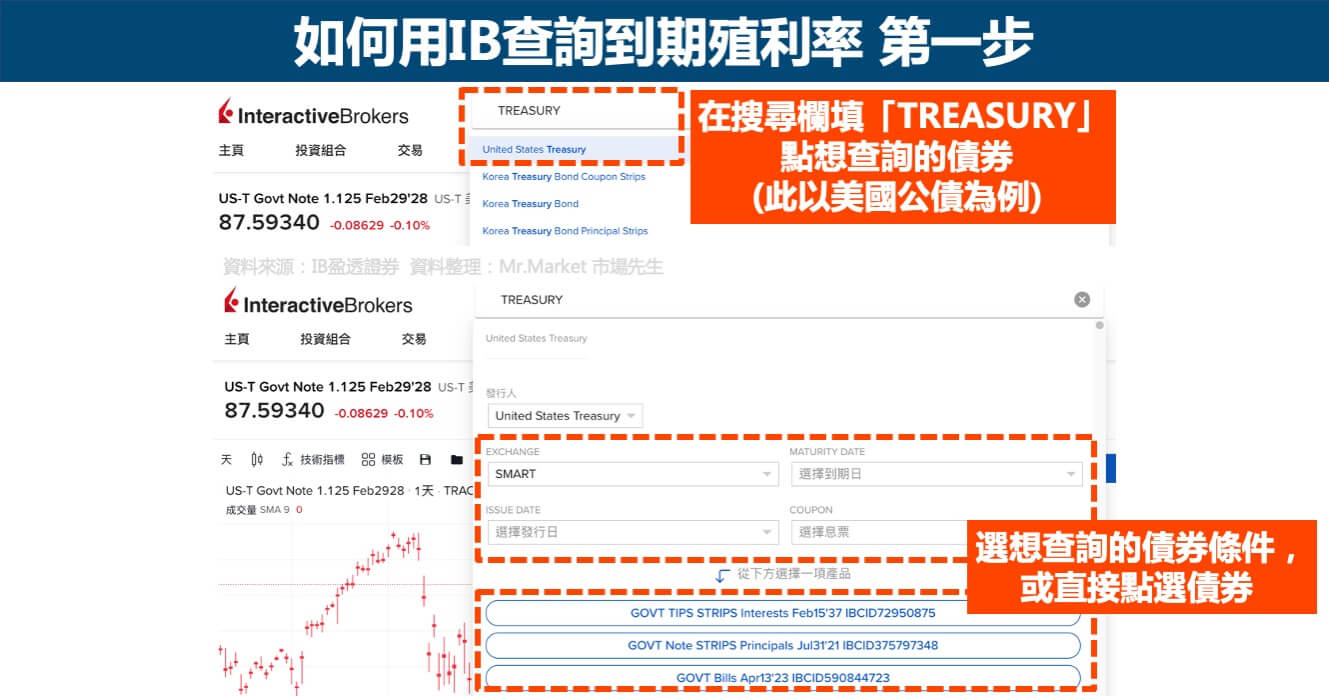
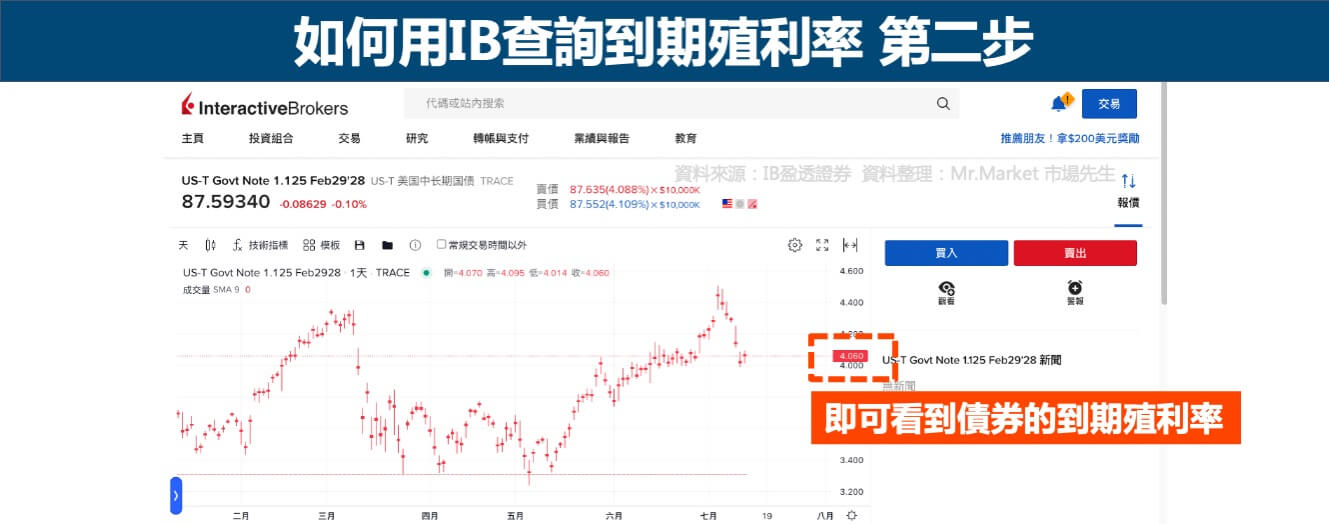
以IB來說,只查得到債券的到期殖利率(這個也是重點),總共兩個步驟,如下圖:
快速重點整理:債券的票面利率、當期殖利率、到期殖利率、贖回殖利率
- 買進債券時要看到期殖利率(YTM),在持有期間要出售則是要看贖回殖利率(YTC)。
- 不要看票面利率跟當期殖利率買賣債券,這兩個數字在投資上沒意義。如果理專跟你說票面利率,那很大可能是話術。
- 決定債券是否要出售,不是只看有沒有賺到錢,還要看贖回金額是否有更好的再投資機會,整體效益是否大於把債券持有到期。
本文為資訊整理與觀念教學分享,無任何投資推薦之意,投資必定有風險,投資前務必自行研究分析判斷。
債券其實是個很好用的投資工具,但也必須正確使用才行,更多債券文章可閱讀:
2. 認識5檔美國公債ETF
專欄作者:牟均俞 主編:市場先生
加入市場先生FB社團,充實更多理財好知識 50歲之前想退休一定要懂理財,解決投資的煩惱!
如果覺得這篇文章有幫助,
幫我按個讚,分享給更多人看到,謝謝!




請問一般新聞提到的美國十年期公債殖利率,指的是當期殖利率還是到期殖利率?
您好,指的是到期殖利率喔,謝謝~
如果買債卷是為了拿債息當退休金,那當期殖利率應該也很重要吧? 那是可以拿到現金當生活費的錢不是嗎?
可以,
畢竟債券定價也都是很效率,所以從同風險債券中,YTM基本也高度近似,你如果是想退休可以從中去挑高當期殖利率的。
我想問一下 大家都說買美債要看YTM,但是我想到一個問題。
這個YTM是假設我把每次收到的利息再投資到相同報酬率的商品上,但是實際上根本很難對吧?
明年如果配息 100塊 這一百塊也買不到公債,或是那時候已經不是高利率。
所以我還要相信這個YTM嗎? 還是直接看票面利率 還是買那種零息債券比較好呢?
1. 說得很好,YTM並沒有辦法假定未來再投資也是一樣的報酬。
但雖然如此,它也是評估當下投資最合適的方式,儘管那不是最後真正拿到的。
而只用真正拿到的去評估,因為不同債券定價、配息都不一樣,不考慮再投資反而無法正確比較。
這也是為什麼不能只看票面利率。
2. 很多人說,債券報酬確定、債券ETF不確定,但那是幫助理解的理論,實際上並非如此。
實際上如果你要考慮實際未來的再投資行為進去,那債券跟債券ETF其實沒什麼不同。
謝謝你的回覆。
如果不考慮股利再投資的部份,我現在買的一檔美國國債,我要怎麼知道半年後他會配多少息給我呢?
還是就是這個3.875%
COUPON: 3.875
每半年配息
Price: 95.126
Principal: 14268.90
Accrued Interest: 146.89
Total Dollars: $14,415.79
3.875% 去乘上面額(例如1000美元),再除以配息頻率(例如半年配一次,一年就是配2次,那就是除以2),就可以得知配息金額。
謝謝! 我明白了!
如果想要避免小白說的再投入導致YTM失準
是否可買STRIP來操作
只是缺點就是無穩定現金流, 必須等到期一次領出
我是覺得沒有所謂YTM失準問題。
YTM如果只是從一個時間點去看,的確會有一個數字。
但並不是說偏離這數字就有錯,
如果你從一整個人生投資週期去看,它不會是一個數字,而是會隨著當下新的利率去變動。
請問是不是可以理解成 在不考慮議價及每年內扣成本的情況下 同一時間買入的債劵ETF 跟同一時間買進的 同樣存續期間的直債 同樣都不再投入 或者同樣都再投入自己的話 在未來任何一個時間會有樣的YTM或YTC嗎?
同樣都再投入,結果會一樣
你好,請教一下
YTM的計算是納入每次配息再投入,並獲得一樣報酬的結果。
那有配息完全不再投入的年化算法嗎?因為可能很多人是領了就拿去使用了。
聽起來這樣沒意義,因為那就不是真正的報酬率,也無法被拿來和其他投資機會互相比較。
拿去用與否,並不影響能不能正確計算一個商品考慮時間價值後的報酬率。
您好
請問一下
面額*票面利率=一年該收取的利息
每家銀行都是照這個公式的嗎?
是喔,債券都是這個規定。利率是年利率,如果有配息2次,那每次就除以二
你好,請問859B殖利率4.27%,平均票息率3.27%這2個那一個才是最重要的配息率?
債券ETF,直接看特性,
例如你提到的就是極短債(1年內),報酬其實就是接近美國短期利率 (美元報酬,要再經過匯率換算但一般不考慮),短債本身回檔就很低。
所以我自己的習慣,是會去看當下最新美債短期利率(3個月、6個月、1年),來判斷它未來的報酬的可能範圍(指美元計價情況下)。而不會去看上面殖利率數字。
尤其是像短債這種,當Fed升降息,過去歷史的數字也不能用在未來。